Ús d'un psicròmetre per a mesurar la humitat relativa del aire

Sobre la consideración de un hilo que da la vuelta a la Tierra ...

Romanesco

Un estiu vaig fer aquesta fotografia a una col que vam plantar a l'hort de casa i que, naturament, ens vam menjar molt a gust. Com veieu és un romanesco, la forma del qual és un exemple emblemàtic d'una fractal. El romanesco Brassica oleracea és un híbrid entre el bròquil (Brassica oleracea var botrytis) i el bròcoli (Brassica oleracea var italica).

La extraordinaria precisión en la medida del radio del protón

La medida más precisa del radio del protón que se ha obtenido hasta el momento presente, mediante es estudio del espectro del hidrógeno excitado, es de $0,833\,\pm\,0,010$ femtómetros ( recordemos que 1 femtómetro = $10^{-15}\,\text{m}$ ). Como ya sabemos, quiere decir ésto que el radio del protón está en el intervalo de incertidumbre $(0,833-0,010\,,\,0,833+0,010)$ femtómetros, esto es, tiene un valor comprendido entre $0,823\times 10^{-15}\,\text{m}$ y $0,843\times 10^{-15}\,\text{m}$ . Podéis leer más acerca de ello en el número de diciembre de 2019, N.º 519, de la revista Investigación y Ciencia, pp. 5-7.

Polipastos

Nota preliminar: teoria (condicions ideals) y pràctica. Elements que resten eficàcia al sistema com a màquina que és (disminució del rendiment teòric)

Les raons de desmultiplicació dels muntatges que apareixen en las figuras son teòriques, car, a la pràctica, mai ses verifican las condicions ideals, degut a les aceleracions que apareixen a l'hora de traccionar; a més, en aquest sentit, encara que només es tracti de retenir la càrrega, les cordes tenen una cierta elasticitat (no son completament estàtiques), las direccions de treball dels trams de corda no sempre són paral·leles; existen fregaments, y, per descomptat, les politges tenen massa (i amb el fregament, giren); todo plegat es tradueix en una pèrdua de rendiment.

-oOo-

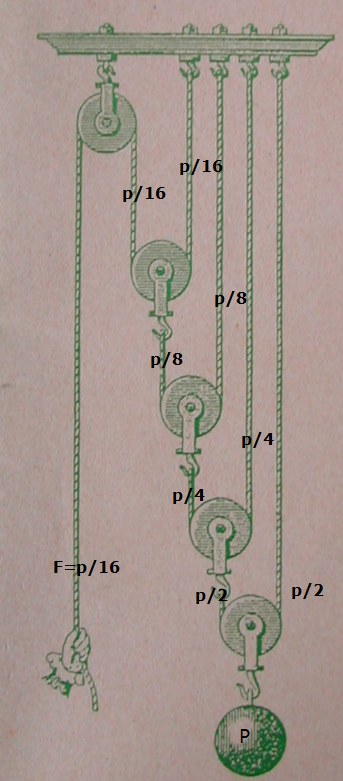
No cal recordar la importància que prenen els sistemes de desmultiplicació de forces. En aquestes notes, repassaré alguns dels conceptes més importants. Fig. 1 Una corda és en medi continu: una tensió es transmet per igual a tots els altres punts. A la figura 1 es mostra un acoblament de politges (polipast) que serveix per mantenir en equilibri un pes P (a la dreta) estirant del tram de corda a l'extrem esquerra amb una força més petita que P. Per simple aritmètica de repartiment de forces, si analitzem el sistema, partint del pes que penja i seguint de baix a dalt i de dreta a esquerra, trobem que la força es divideix per dos cada vegada que ens trobem amb una nova politja; arribem, doncs, a la conclusió que només caldrà fer una força igual a 1/16 del pes del cos per mantenir el sistema en equilibri. És per això que parlem d'un sistema reductor (o desmultiplicador) amb una relació nominal 1:16 Els següent polipast té una relació nominal 1:4 (figura 2). Els 100 N es reparteixen per igual entre cadascun dels quatre trams que connecten la politja superior (fixa) i el quadernal (la politja mòbil). Fig. 2 Polipast de relació nominal 1:4 (font: Wikipedia)http://upload.wikimedia.org/wikipedia/commons/2/2a/Polispasto4.jpg La imatge següent (Figura 3.) mostra diversos tipus de polipastos que s'utilizen sovint en velers. A la part superior de cada un hi anatada la relació nominal. Fig. 3 (font de la imatge: C. Wing, Cómo funcionan las cosas de los barcos, Tutor, 2005) $\diamond$

-oOo-

Lecturas complementarias sugeridas:

  [1] En mi blog de montaña: Polipastos en escalada/alpinismo para rescate y autorrescate, 2023.

Formas de crecer y aprovechar la luz

Buitrago del Lozoya, primavera de 2021

El nonio: la maravillosa invención de Pierre Vernier (1580-1637)

El nonius (nonio) o vernier (1) sirve para mejorar la sensibilidad de los aparatos que se utilizan para la medida de longitudes. La misma idea se aplica para aumentar la sensibilidad de los aparatos que sirven para medir amplitudes angulares. Unos cuantos ejemplos muy conocidos del uso del vernier son el pie de rey (o calibre), el palmer (o micrómetro), en un sextante, el teodolito, o el goniómetro con nonius (muy necesario en muchas máquinas herramientas, como las fresadoras, para el mecanizado de piezas de precisión).

    Un nonius consiste en una regla (dividida en partes iguales) sobre la que se hace deslizar una reglilla/nonius (dividida también con su propia graduación, también en partes iguales) de manera que $n_r-1$ divisiones de la regla comprendan $n_N$ divisiones de la reglilla o nonius, por lo que la longitud de cada división del nonius, $d_N$, es algo más pequeña que la de cada división de la reglilla, $D_r$. Así, la sensibilidad, $s$, que obtenemos viene dada por la diferencia $D_r-d_N$; donde, lógicamente, $d_{N}\cdot n_r$ ha de ser igual a $D_{r}\cdot (n_r-1)$, luego la longitud de cada división del nonius viene dada por $$d_N=\dfrac{D_{r}\cdot (n_{r}-1)}{n_N}$$
    Con el añadido del nonius a la reglilla, la sensibilidad que conseguimos se deduce ahora fácilmente $$s:=D_r-d_N=D-\dfrac{D_{r}\cdot (n_{r}-1)}{n_N}=\dfrac{D_r}{n_N}$$ mientras que, sin la incorporación del nonius, dicha sensibilidad sería en tal caso la de una unidad de la regla, esto es, $s_{\text{regla}}=D_r=1\,\text{mm}$, una sensibilidad grosera, que se afina mucho más con el uso del nonius: $s_{\text{pie de rey}}\dfrac{D_r}{n_N}\lt 1$, por ser $n_{N}$>1
    Así, por ejemplo, un pie de rey en el que el nonius conste de $n_N=50$ divisiones, siendo $D_r=1\,\text{mm}$ (la longitud de cada división de la regla), logramos una sensibilidad $s_{\text{pie de rey}}=\dfrac{1}{50}\,\text{mm}=0,02\,\text{mm}$ (dos centésimas de milímetro).

    Tanto la amplitud máxima de medida del pie de rey (máximo desplazamiento de la reglilla/nonius sobre la regla) como la sensibilidad vienen grabadas en el aparato de la forma «amplitud x sensibilidad». Por ejemplo, en el pie de rey que tengo encima de mi mesa leo «$150\times 0.02\,\text{mm}$»; la primera cantidad es la amplitud máxima de medida (puedo medir longitudes que no sean mayores que «150 mm», con una sensibilidad de $2$ centésimas de milímetro.
    Acabemos haciendo una generalización. Lo dicho anteriormente acerca de que $n_{r}-1$ divisiones de la regla comprendan $n_N$ divisiones del nonius puede generalizarse: podemos diseñar un nonius de tal manera que $n_r$ divisiones de la regla comprendan $m_N$ divisiones del nonius; donde, lógicamente, tengamos que $m_{N}\gt n_r$. Con lo cual, la expresión que nos da la sensibilidad es, en general, $$s:=D_r-d_N=D_r-\dfrac{D_{r}\cdot n_{r}}{n_N}=\dfrac{D_{r}\cdot (n_{N}-n_r)}{n_N}$$ en particular, si $n_r=n_N-1$ recuperamos lo que arriba hemos descrito. $\square$

-oOo-
Notas:
    (1) Pierre Vernier (1580-1637), matemático francés que mejoró la sensibilidad de los instrumentos de medida de longitudes y ángulos, gracias al dispositivo que ideó para todos ellos, el nonius (o vernier<(i>) el cual consiste en una subescala superpuesta a la escala principial. Ejemplos de dichos instrumentos son el pie de rey, el palmer (o micrómetro), y los goniómetros de precisión.
-oOo-
Referencias:
    [1] BURBANO, S. et. al., Física General, Tébar, Madrid, 2007 (32ª edición)
    [2] BURBANO, S. et. al., Problemas de Física, Tébar, Madrid, 2007 (27ª edición)
    [3] vv.aa., Nonio, Wikipedia [https://es.wikipedia.org/wiki/Nonio]
    [4] vv.aa., Pierre Vernier, Wikipedia [https://fr.wikipedia.org/wiki/Pierre_Vernier_(mathématicien)]
    [5] vv.aa., Consulta de diversos instrumentos de medida, con las siguientes palabras clave: pie de rey, palmer, teodolito, goniómetro, etc., Wikipedia

Quatre coses essencials sobre un aparell/sistema de mesura: sensibilitat, precisió, exactitud, i rapidesa

Quan hom parla d'un aparell/sistema de mesura cal tenir ben en compte quatre nocions essencials: la sensibilitat, la precisió, l'exactitud, i la rapidesa.

Sensibilitat
    La sensibilitat d’un aparell de mesura es refereix al valor mínim de quantitat mesurada que és capaç de discriminar.

Precisió
    Donat un determinat aparell de mesura, que farem servir per mesurar el valor d'una determinada magnitud, convindrem que si la diferència entre diverses mesures (d'una sèrie) d’aquesta mateixa magnitud és petita, l'aparell és precís.

Observació:
    Per a cada cada tipus de mitjà de mesura s'ha convingut un límit d’error acceptable que dóna lloca a la noció de classes de precisió dels mitjans de mesura, terme que es pot trobar sovint als manuals de metrologia.

Exactitud
    Direm que un aparell és prou exacte si el promig d'una sèrie de mesures que es realitzen amb aquest aparell és prou proper al valor considerat com a valor exacte/vertader de la magnitud mesurada.

Observació:
    Per bé que exactitud implica precisió, la precisió no necessàriament implica l'exactitud, degut als errors sistemàtics. És, per això, que és molt més fàcil valorar la precisió d’un instrument/sistema de mesura que no pas la seva exactitud.

Rapidesa
    La rapidesa en la mesura pot arribar a ser essencial a l'hora de prendre mesures en temps real per fer un registre d'una sèrie temporal i així poder enregistrar els valors d'una determinada variable d’un sistema dinàmic. Si el dispositiu de mesura no és prou ràpid és possible que el registre temporal dels valors de la dita variable del sistema estiguin desplaçats en el temps d'una manera imponderable, ja que, d’entrada, hom no disposa d'informació sobre el ritme de canvi entre els estats del sistema. $\square$

-oOo-
Referències:
    [1] vv.aa., Precición y exactitud
      [https://es.wikipedia.org/wiki/Precisión_y_exactitud], Wikipedia , 2008
    [2] ARANES CLUA, J., Els errors en les mesures directes, autopublicació, 2008
    [3] PROJOROV, A.M., Diccionario enciclopédico de la Física, Madrid, Mir-Rubiños, 1995
    [4] AZUSTRE, M. et al. Estadística aplicada al laboratori, Barcelona, Ceysa, 2003.

Cantidades que resultan de las mediciones. Acerca de la cifra/dígito menos significativa

Los dígitos de las cantidades obtenidas (números en base decimal) como resultado de las mediciones se denominan cifras significativas. Si por ejemplo, se ha medido la longitud del lado de una mesa, obteniendo el valor $121\,\text{cm}$ diremos que ésta tiene tres cifras significativas (3 c.s.); y si la hemos medido con un instrumento capaz de afinar hasta los milímetros, obteniendo el valor $121,4$, diremos que el resultado de dicha medida tiene cuatro cifras significativas (4 c.s.). En este contexto, hablemos ahora de qué debemos entender por la cifra menos significativa de una cierta cantidad.

Cifra menos significativa en el caso de tratarse de un número entero
    La cifra menos significativa de un número entero es el dígito que tiene el menor valor posicional, es decir, la que está situada más a la derecha; así, por ejemplo, la cifra menos significativa del número $234$ es el «4», ya que es la que está más a la derecha y es distinta de cero (la cifra de las unidades en este caso); sin embargo, entenderemos —como norma general— que los ceros a la derecha de una cantidad entera (medida) no son cifras significativas; así, por ejemplo, la cifra menos significativa de la cantidad (medida) $520$ es el «2» (la de las decenas, en este caso), por ser cero la última cifra a la derecha.
    No obstante, bien pudiera ser que, por motivos plenamente justificados por el resultado de la medida, algunos de esos ceros a la derecha sí fuesen cifras significativas. En tal caso, lo notaremos escribiendo una coma decimal a la derecha del último cero; así, por ejemplo, si queremos dar a entender que el «0» de dicha cantidad sí es una cifra signicativa, y por ello escribiremos $520,$ en lugar de $520$.

Observación:
    En computación y, concretamente, en programación de microcontroladores (a bajo nivel), cabe señalar que, al operar habitualmente en el sistema de numeración binaria, los bits «0» tienen tanta validez y consideración como los bits «1», como és bien claro. En ese contexto —no hablamos ahora de medidas, sino al procesado numérico de los datos— nos referimos a los bits por su peso posicional, del de mayor al de menor peso, del primero a la izquierda (el más significativo o de mayor peso posicional) al último a la derecha (el menos significativo o de menor peso posicional).


Cifra menos significativa en el caso de tratarse de un número decimal
    Ahora bien, hay que tener en cuenta que si el número es decimal, el cero a la derecha de la parte decimal, de haberlo, sí que, en cualquier caso, también cuenta como cifra significativa; así, por ejemplo, diremos que la cifra menos significativa del número $2,680$ es el «0» (cifra de las milésimas, en este caso).$\square$

-oOo-
Referencias:
    [1] ATKINS, P.;L. JONES, Chemical Principles. The Quest for insight, Freeman, NY, 2005. [Existe una traducción al castellano: Principios de Química (3ª edición, 1ª reimpresión), Panamericana, 2007]

Un polipasto

Cristales y álgebra

[Teoría de grupos aplicada a la Cristalografía (2015)]

Leyendo datos numéricos de un archivo. Un programa sencillo en C

//
// Aquest programa recupera n dades numèriques
// d'un fitxer de disc
// Joan Aranès Clua (1992)
//
#include <stdio.h>
#include <string.h>
#include <conio.h>
main()
  {
    FILE *fp;
    int i,n;
    float a;
    float v[10];
    char s[80];

    clrscr();
    printf("nom del fitxer que vols recuperar?\n ");gets(s);
    printf("nombre de dades numèriques ?\n");scanf("%d",&n);

    fp=fopen(s,"r+t");
    for(i=0;i<n;++i)
      {
	fscanf(fp,"%f\n",&v[i]);
	printf("\nv[%d]=%f",i,v[i]);
      }

    fclose(fp);
    printf("\nLectura efectuada");
    getch();
}

Escribiendo datos numéricos en un archivo. Un programa en C.

// Aquest programa escriu n dades numèriques
// en un fitxer de disc
// Joan Aranès Clua (1992)
//
#include <stdio.h>
#include <string.h>
#include <conio.h>
main()
  {
    FILE *fp;
    int i,n;
    float a;
    float v[10];
    char s[80];

    clrscr();
    printf("nom del fitxer ?\n ");gets(s);
    printf("nombre de dades numèriques ?\n");scanf("%d",&n);

    fp=fopen(s,"w+t");
    for(i=0;i<<n;++i)
      {
	printf("v[%d]=",i);scanf("%f",&v[i]);
	fprintf(fp,"%f\n",v[i]);
      }

    fclose(fp);
    printf("\nDades guardades en el fitxer de disc");
    getch();
 }
 

Llei de radiació de Planck (1900)

//-----------------------------------------------------------------
// radiació del cos negre 
//
// Joan Aranès Clua
// data: 13/12/2001
// 
// Aquest programa calcula la densitat d'energia per unitat de volum
// (en Joule/m^3) a partir de la longitud d'ona 
//de la radiació (en metres) i de la temperatura 
// (en graus Kelvin) d'un "cos negre" - llei de radiació de Planck (1900) -

// estimació dels ordres de magnitud: 
// Pera una longitud d'ona -> 2*10^-7 m
// i una temperatura de radiació: de 2*10^3 K
// cal esperar una densitat d'energia de l'ordre de 10^-6 Joule/m^2
//
// el fitxer adicional ll_planck.jpg mostra una representació en 3D 
// d'aquesta funció (densitat d'energia (z) 
// amb les dues variables independents (lambda (x) i temperatura (y) 
// construïda amb el programa DERIVE
//-----------------------------------------------------------------


// definició de les constants físiques
#define PI 3.1416
#define _h 6.6256E-34
#define _c 2.9979E8
#define _k 1.3805E-23

// llibreries
#include <stdio.h>
#include <math.h> //pow() i exp()



void main()
{

    double T,lambda;//variables d'entrada
	double densitat; //variable de sortida

    printf("introdu\x08Bu el valor de la temperatura en graus Kelvin:\n");
    scanf("%lf",&T);

    printf("introdu\x08Bu la longitud d'ona en m:\n");
    scanf("%lf",&lambda); 
	
	//-------------------------------------------
	// càlcul de la densitat
	densitat=8*_h*_c/pow(lambda,5);
    densitat=densitat/(exp(_h*_c/lambda/_k/T)-1); 
	//-------------------------------------------
	
	printf("densitat d'energia monocrom\x085tica:%e\n",densitat);    

}

Temas de reflexión sobre fotografía conceptual: "Información, tiempo, materia y energía"

[Altafulla, en algún momento de 2018]

Tensión superficial

La tensión superficial permite que las gotas de agua de una reciente lluvia permanezcan en las hojas de las plantas adoptando una forma casi esférica
Referencias:
  [1] https://es.wikipedia.org/wiki/Tensión_superficial, Wikipedia

Antenas

Las antenas constituyen un interesante campo de estudio para la trasmisión y recepción de ondas electromagnéticas. Voy a ir escribiendo artículos sobre ello. La fotografía de la Fig. 1 la tomé en un pueblo de la Sierra Norte. Dicha antena de televisión está orienda hacia la antena repetidora que está situada en lo alto de una colina. Podemos observar la rejilla conectada a tierra que permite mejorar la ganancia con respecto a una antena dipolar simple.

Fig. 1 - Antena UFH de TV -ooO- Referencias para una introducción al tema:
  [1] https://es.wikipedia.org/wiki/Antena, Wikipedia

¿ Qué es la tasa metabólica ?

    El gasto mínimo de energía para que una persona mantenga sus procesos vitales es, de manera orientativa, alrededor de $65\,\dfrac{\text{kcal}}{\text{h}}$( tasa de metabolismo basal, TMB [1] ); si bien, cada persona tiene su propio valor según sus características, dependiendo éste del género, el peso, la estatura, la edad, tipo de actividad, temperatura ambiente, así como de otros factores [2] . Para medirlo con una cierta precisión, ésta debe estar en reposo, en ayunas y a una tempertura ambiente de $20^\circ\,\text{C}$

Según va aumentando la necesidad de energía para realizar actividades cada vez más exigentes, el valor de la TMB se multiplica por un factor, $\alpha$, que da cuenta del aumento en de la energía requerida. Para la actividad mínima, dicho factor es, desde luego, igual a 1; y según aumenta la exigencia energética por la actividad que se realice, el coeficiente de variación puede variar hasta valores extremos superiores a 5.

Por tanto la cantidad de energía requerida, $\mathcal{E}$, según las distintas etapas de actividad a lo largo de un día, puede expresarse de la forma $$\mathcal{E}=\text{TMB}\cdot ( \alpha_1\cdot t_1+\alpha_2\cdot t_2+\ldots+\alpha_n\cdot t_n),\;\text{donde}\; t_1+t_2+\ldots+t_n=24\,\text{horas}$$ Sugerencia: Este cómputo puede realizarse cómodamente con una hoja de cálculo.

Así, por ejemplo, la actividad física para un deportista exigente puede llegar aproximarse a $\alpha=4$, con un gasto diario cercano a las $4000\,\text{kcal}$ en un día, y un alpinista o un navegante oceánico a vela puede llegar a superar un valor de $10$, y requererir por tanto una cantidad de energía que puede alcanzar las $8000\,\text{kcal}$ al día.




-oOo-
ENUNCIADO
¿ Cuál es el gasto energético diario para una persona cuya tasa de metabolismo basal (TMB) es de 65 kcal/h si realiza una actividad principial que, teniendo en cuenta las horas de descanso y de sueño, se estima ( en la media del día ) en un factor $\alpha=2$ ?.
Exprésese también dicho resultado en kilojoules. Recordemos que el joule, J, es la unidad de energía del Sistema Internacional ( abreviado, SI ), y que 1 kcal = 4,184 kJ

SOLUCIÓN
Basta multiplicar la TBM por el coeficiente de variación y por $24\,\text{h}$ ( 1 día = 24 h ), esto es, convirtiendo kilojoules ( kJ ) el resultado del cálculo en kilocalorías ( kcal ). Así se obtiene
$$65\,\dfrac{\text{kcal}}{\text{h}}\cdot 2 \cdot \,\dfrac{24}{1}\,\dfrac{\text{h}}{\text{día}}\approx 3\,120\,\text{kcal}$$
$$65\,\dfrac{\text{kcal}}{\text{h}}\cdot 4,184 \,\dfrac{\text{kJ}}{\text{kcal}} \cdot 2 \cdot \,\dfrac{24}{1}\,\dfrac{\text{h}}{\text{día}}\approx 13\,054\,\text{kJ}$$


-oOo-
Observaciones:
(1) Antiguamente, en el ámbito de la nutrición y las ciencias de los alimentos se usaba la llamada Caloría ( abreviado, Cal ), y hay que tener en cuenta que $1\,\text{Cal} = 1000\, \text{cal} = 1\, \text{kcal} = 4,184\, \text{kJ}$

Referencias:
[1] Tasa metabólica basal ( [ https://es.wikipedia.org/wiki/Tasa_metabólica_basal ], Wikipedia )
[2] Tabla para estimar la TMB según la edad, el peso, el género y otros factores ( [http://www.fao.org/3/w0073s/w0073s0c.htm] )
$\square$.

El ahorro de energía es un imperativo

La capacidad de carga eléctrica de una batería se suele expresar en $\text{Ah}$, lo cual facilita muchos cálculos. La batería de servicio en un pequeño velero suele tener una capacidad de $70\,\text{Ah}$. Las baterías de servicio se pueden cargar mediante el alternador del motor auxiliar, o también mediante paneles fotovoltaicos.

    Vamos a considerar una situación de avería. Supondremos que no tenemos paneles fotovoltaicos para recargar la batería de servicio, y que tenemos una avería en el alternador, de manera que tampoco es posible cargarla teniendo en funcionamiento el motor auxiliar.


-oOo-
ENUNCIADO
En las condiciones descritas arriba, nos encontramos con la batería de servicio medio cargada, con una carga almacenada de $35\,\text{Ah}$. Cae la noche, y tenemos que encender las luces de navegación las cuales requieren una potencia de $23\,\text{W}$; también deseamos mantener encendida la emisora VHF; decidimos tenerla a mínima potencia ( sólo a la escucha ), por lo que contamos con que demandará $1\,\text{W}$ de potencia. ¿ Para cuánto tiempo tendremos energía ?.

SOLUCIÓN
Todas las cargas ( lámparas, la emisora, etcétera ) suelen estar conectadas en paralelo a los borne de la batería, entre los cuales hay una tensión de $12\,\text{V}$. La potencia total requerida ( de la carga equivalente ) es $P=23\,\text{W}+1\,\text{W}=24\,\text{W}$. Como la potencia disipada en la carga se calcula multiplicando la tensión ( entre bornes ) por la intensidad de corriente eléctrica, podemos escribir que $24=12\,I$, luego la intensidad total de corriente requerida es $I=\dfrac{24}{12}=2\,\text{A}$. Entonces, como la carga almacenada en la batería es de $35\,\text{Ah}$, basta una simple proporción directa para calcular el tiempo pedido, que será igual a $\dfrac{35\,\text{Ah}}{2\,\text{A}}=17,5\,\text{h}=17\,\text{h}\,30\,\text{min}$
$\square$

Acerca de la energía que gastamos al correr una maratón

En maratones corridas entre $4\,\text{h}\;,10\,\text{min}$ y $5\,\text{h}\;,15\,\text{min}$ el kilómetro, se estima que, por término medio, el gasto energético puede ser calculado a razón de $1\,\text{kcal}$ por cada kilogramo de masa y por kilómetro recorrido.
-oOo-
ENUNCIADO
Teniendo en cuenta la información arriba indicada, queremos calcular la cantidad de energía que requiere una corredora de maratón ( el corrido de una maratón es de $42,195\,\text{m}$ que tiene una masa de $60\,\text{kg}$. En la cuestión número 1 hablamos de la tasa metabólica basal (TMB) - energía mínima necesaria para mantener los procesos vitales en el ser humano -, y cuyo valor situábamos alrededor de $65\,\dfrac{\text{kcal}}{\text{h}}$, y comentábamos que para actividades que requieren més energía que ésa, podemos calcular (de manera aproximada) la energía que se necesita en conjunto multiplicando la TBM por un factor $\alpha$ ( propio del tipo de actividad ). ¿ Cuál es el valor de dicho factor en la situación descrita ?

SOLUCIÓN
Teniendo en cuenta la relación de proporcionalidad directa entre la energía requerida y la logitud de camino recorrido, así como entre dicha energía y la masa de la corredora, podemos calcularlo fácilmente:
$\mathcal{E}=1\,\dfrac{\text{kcal}}{\text{km}\,\text{kg}}\cdot 60\,\text{kg}\cdot 42,195\,\text{km}\approx 2\,532\,\text{kcal}$

Para responder a la segunda pregunta ( ya suponemos que el valor de dicho factor tiene que ser bastante alto ) basta plantear la siguiente ecuación: $2\,532 = 65\cdot \alpha \cdot t \quad \quad (1)$, donde $t$ es el tiempo que dura la actividad, esto es, el tiempo que necesita para terminar el recorrido. Así que, primero, vamos a calcular cuánto tiempo necesita la corredora. Para ello, supondremos que, en media, necesita $5\,\text{min}$ para recorrer $1\, \text{km}$. Así, $t=42,195\,\text{km}\cdot \dfrac{5}{1}\,\dfrac{\text{min}}{\text{km}}\approx 211 \,\text{min} \approx 3,5 \,\text{h}$

Por tanto, de (1): $2\,532 = 65\cdot 3,5\, \alpha$, luego $\alpha=\dfrac{2\,532}{65\cdot 3,5} \approx 11$, que es un valor muy alto, como era de prever.
$\square$

Pedaleando en la bicicleta estática a la luz de un humilde leño que arde en el hogar

    La leña que arde en la chimenea o en la estufa tiene un poder calorífico de unos 4200 Wh por kilogramo. Naturalmente este es un valor indicativo, pues dependerá del tipo de leña. Así, un leño de 1 kg de masa que arde lentamente durante 1 hora proporciona una energía calorífica de 4200 Wh = 4,2 kWh.
-oOo-
ENUNCIADO
Consideremos el gasto energético de una persona que realiza ejercicio físico pedalenado en su bicicleta estática intenso durante 1 hora, mientras el leño arde en el hogar una tarde de invierno. Pongamos que dicho ejercicio físico realizado durante esa hora requiere unas 340 kcal de energía química ( que proporciona nuestro metabolismo). ¿ En qué medida podemos comparar este gasto de energía con la que proporciona nuestro leño al arder durante esa hora en la chimenea ?

SOLUCIÓN
Recordemos que 1 kcal equivale 4,184 kJ, esto es 1 kcal = 4,184 kWs = 4,184/3600 kWh $\approx 4,2/3600$ kWh $\approx 0,0012 \,\text{kWh}$, luego 340 kcal = 0,408 kWh. Entonces la energía que proporciona nuestro humilde leño es 4,2/0,408 $\approx 10$ veces la cantidad de energía requerida para realizar esa actividad física intensa en la bicicleta.


-oOo-
Observaciones/reflexiones:
Pensemos que nuestros antepasados, antes de que aprediésen a encender el fuego, tenían una capacidad de extraer energía de su entorno que se reducía a la propia de su metabolismo. Al empezar a encender el fuego multiplicaron por 10 esa capacidad, lo cual, sin duda, supuso un cambio significativo en la evolución cultural de las sociedades humanas. Si contamos los anillos de crecimiento del leño, podemos contabilizar los años transcurridos hasta el momento del corte del leñador para proporcionarnos el combustible que está ardiendo en el hogar; posiblemente contaremos más de 10 anillos, que son 10 años ( 1 anillo por año ). Estos pensamientos nos sumirán seguramente en ensoñaciones sobre la capacidad que tenemos los seres humanos para manejar grandes cantidades de energía. Hemos hablado de la leña ( la madera ), que tiene un poder calorífico aproximado de unos 4 kWh/kg ( el de los pellets es de unos 6 kWh/kg ); los combustibles fósiles tienen un poder calorífico unas tres veces superior al de la madera: el del butano y propano, ronda los 14 kWh/kg; y el del gasoil de calefacción es aproximadamente de 11 kWh/kg. Sin embargo, han tenido que pasar millones de años para que se formasen esos depósitos de hidrocarburos. Ya véis que da para mucho una hora de ejercicio físico a la luz del humilde leño que arde lentamente en el hogar. Y ya no hablamos de la energía nuclear: 1 kg de uranio en la reacción de fisión libera $2\times 10^6$ veces la energía de 1 kg de gasoil. Eso da vértigo, ciertamente. Y también miedo, seamos francos.

Referencias:
[1] Poder calorífico ( [ https://es.wikipedia.org/wiki/Poder_calorífico ], Wikipedia )
$\square$.

Bicicletas eléctricas

    El motor eléctrico que se suele encontrar en las bicicletas eléctrica tiene una potencia aproximada de 250 W - un taladro de mano tiene más potencia, alrededor de los 750 W -. Las baterías ( de diversa tecnología ) suelen tener una capacidad de 20 Ah, y la tensión entre bornes del motor suele ser de 24 V.
-oOo-
ENUNCIADO
Considerando la información ( orientativa ) proporcionada arriba, ¿ Cuál es el valor máximo de la autonomía de una bicicleta eléctrica ( de las características descritas ) ?

SOLUCIÓN
Si nos imaginamos montando en llano, sin pedalear, y dejándo por tanto todo el trabajo al motor eléctrico ( tampoco le ayudamos en nada a cargar la batería con el pedaleo y el alternador ), podemos calcular el tiempo que estaremos rodando hasta que la batería se agote dividiendo la capacidad de la batería ( en Ah ) por la intensidad de corriente de trabajo del motor ( en A ); así que tendremos que calcular primero dicha intensidad: como la potencia es igual a la tensión por la intensidad, tenemos que esa intesidad es igual a 250 W / 24 V approx 10 A. Luego el tiempo pedido es igual a 20 Ah / 10 A = 2 h


-oOo-
Observaciones/reflexiones:
Si bien la bicicleta eléctrica es una buena alternativa a los vehículos pequeños ( y grandes ) con motores de combustión, pensomos que las baterías tienen que recargarse en casa, enchufándolas a la red eléctrica. Cobra pues mucha importancia la fuente ( o fuentes de energía ) que utilizamos para cargar esas baterías. Si proceden de centrales térmicas, habremos hecho un pan con unas tortas. Ahora bien, recordemos que un trabajo algo exigente en bicicleta sin motor requiere unas 350 kcal/h, así que en 2 horas, supondrá una demanda a nuestra energía química de entre 600 y 700 kcal, que es menor que la energía requerida por el motor eléctrico; en efecto: 250 W · 2 h = 0,5 kWh · (1/0,00116 ) kcal/kWh = 431 kcal.

El lector habrá observado que la intensidad de corriente que alimenta el motor eléctrico en una bicicleta es elevada. Debe pues estar bien protegido el sistema, para evitar riesgos de electrocución. Así pues, mucho cuidado al manipular el motor con la batería conectada.

Referencias:
[1] Bicicletas eléctricas ( [ https://es.wikipedia.org/wiki/Bicicleta_eléctrica ], Wikipedia )
$\square$.

Airbus A350 - ¿ Cuánto gasta ese trasto ?

    Un Airbus A350 está propulsado por dos enormes motores a reacción. Cada uno de ellos puede llegar a proporcionar una fuerza de empuje aproximada de 3·10^5 N. El avión puede alcanzar una velocidad de crucero de 900 km/h a 12000 m de altitud.
-oOo-
ENUNCIADO
Considerando la información ( orientativa ) proporcionada arriba, ¿ qué cantidad de energía puede llegar a gastar un avión de este tipo ?

SOLUCIÓN
Si nos ponemos en la situación de máximo gasto de energía del avión, basta multiplicar la fuerza por la velocidad para obtener la potencia desarrollada por cada uno de los dos motores: 3·10^5 N · 900 km/h · 1000 m/km · 1/ 3600 h/s = 75 000 000 W = 75 000 kW, y, como tenemos dos motores, la potencia máxima con la que se puede contar es de 150 000 kW. Así que en 1 h de vuelo en estas condiciones, la energía requerida ( del combustible químico ) es de 150 000 kWh


-oOo-
Observaciones/reflexiones:
Vamos a comparar este requerimiento de energía con la de un automóvil utilitario de 100 CV de potencia ( 73,5 kW ). Dividiendo la potencia máxima del Airbus A350 por la del automóvil obtenemos la friolera de 150 000 / 73,5 approx 2041, esto es, el gasto máximo de ese gran avión equivale al gasto máximo de 2041 automóviles. En otro artículo hablaremos de los motores de los cohetes que sitúan en órbita a los satélites. Dicho lo dicho, seguro que nadie se va a sorprender.

Referencias:
[1] Airbus A350 ( https://es.wikipedia.org/wiki/Airbus_A350 ) [2] Unidades de potencia en automoción ( https://neomotor.sport.es/conduccion/potencia-del-coche-a-cuantos-caballos-cv-equivale-un-kilovatio-kw.html ) $\square$.

Instalaciones autónomas de energía eléctrica con paneles fotovoltaicos

Casi en cualquier lugar podemos ver ya instalaciones fotovoltaicas [1] ( viviendas unifamiliares, autocarabanas, viviendas aisladas, embarcaciones, equipos de señalización de tráfico, etcétera ). Por humildes que puedan ser, proporcionan energía eléctrica renovable a partir de la luz. Constan de un panel constituido por un conjunto de células solares dispuestas en serie; a su vez, cada panel puede conectarse con el resto de paneles en serie o bien en paralelo, según las características y necesidades de la instalación. Al conjunto de paneles les llamamos módulo fotovoltaico. Se necesita también un regulador de carga, conectado en paralelo al panel ( o módulo fotovoltaico ) para impedir que las puntas indeseadas en la generación de carga eléctricas y para evitar sobrepasar la máxima capacidad de carga de la batería, la cual, en sí, puede estar formada por un conjunto de unidades conectadas en serie, o en paralelo ( si se requiere almancenar mucha carga eléctrica. La batería suele conectarse directamente al regulador, emplando las conexiones que para ello ya vienen dispuestas en él.

La batería es un elemento imprescindible en un sistema fotovoltaico, pues permite guardar la carga eléctrica que el panel ( o asociación de paneles ) produce, permitiendo así que podamos servirnos de ella cuando el panel no produce electricidad ( de noche, o en tiempo nublado ). A la salida del módulo fotovoltaico se conecta el regulador de carga, al cual también puede conectarse directamente la batería; y, en el caso de que necesitemos corriente alterna, a la salida del regulador, habrá que conectar también un inversor, para convertir la corriente continua (que proporciona la batería) en corriente alterna; así podremos hacer funcionar dispositivos que requieran este tipo de corriente eléctrica ( lavadoras, frigoríficos, televisor, etcétera ), siempre que, claro está, el módulo fotovoltaico tenga la potencia suficiente para tener la carga eléctrica necesaria almacenada en la batería en todo momento. A la hora de diseñar el sistema, la capacidad de la batería ( recordemos que se expresa en amperios-h, abreviado Ah ) se calcula calcula en función de la potencia del módulo fotovoltaico requerida y de las necesidades de consumo de las cargas que se tengan que alimentar.

ENUNCIADO
En un pequeño velero con el que se desea realizar navegación costera con pernoctación a bordo, queremos instalar una neverita de 35 W, un piloto automático de caña de 12 W, las luces de navegación nocturna con 15 W de potencia entre todas ellas. También necesitamos alimentar permanentemente la emisora VHF, que puede requerir una potencia de 5 W, y reservamos 5 W para imprevistos. Para no depender de la carga de la batería de servicio mediante el motor auxiliar y ser lo más autónomos que podamos y así no tener que depender de la alimentación de corriente cuando estemos en puerto, hemos decidido instalar un sistema fotovoltaico. Cada una de estas cargas, que funcionan con corriente continua ( no necesitamos corriente alterna, y, por tanto prescindiremos de la instalación de un inversor ) está conectada en paralelo a una batería de 12 V. ¿ Cuál es la potencia estimada del panel fotovoltaico ? ¿ Y la capacidad de la batería de servicio ( alimentada por el panel fotovoltaico ) ?

SOLUCIÓN
La carga global conectada en paralelo ( circuito equivalente ) requiere una potencia de $35+12+15+5+5 = 72\,\text{W}$, por lo que la intensidad de corriente que pasa por esa carga es de $72\,\text{ W} / 12 \,\text{V} = 6\,\text{A}$. Entonces, necesitaremos una carga eléctrica $6 \cdot 24\text{A h} = 144\, \text{Ah}$, por lo que necesitamos una betería ( o sistema de baterías ) de servicio que tenga una capacidad un poco mayor que este valor, esto es, una batería de $150\,\text{Ah}$ de capacidad. Por lo que respecta al modulo fotovoltaico ( panel o paneles ) puede consister en una sola unidad de $150\,\text{W}$ de potencia; y como la corriente punta ( a máximo rendimiento ) es de $150 \,\text{W} / 12 \,\text{V} = 12,5\,\text{A}$. Necesitaremos por tanto un regulador de carga que pueda gestionar unos $20\,\text{A}$


-oOo-
Observaciones/reflexiones:
Todas las personas aficionadas a la navegación a vela de crucero son muy conscientes de la importancia de no malgastar la electricidad a bordo. Y, por cierto, tampoco el agua potable, pues en una embarcación pequeña las reservas de la misma son muy valiosas.

Referencias:
[1] https://es.wikipedia.org/wiki/Energía_solar_fotovoltaica ( Wikipedia )
$\square$

Interpretando una factura de nuestro proveedor de electricidad

La imagen muestra un recibo típico de la factura de la luz. En él se desglosa el gasto de energía ( expresado en kWh ) del coste del servicio: tasa por contratación de la potencia deseada en la instalación, entre otros conceptos). Notad que el precio del kilowatio-hora es, en este ejemplo, muy elevado; a veces sucede, y, como es comprensible, siempre que ocurre eso hay mucha controversia al respecto.

[Haced clic sobre la imagen para verla en tamaño natural]

Veamos a continuación otro ejemplo idealizado ( por su sencillez ) en el que se remarca el desglose en el coste de los conceptos de los que hemos hablado. Eso sí, hemos hecho un supuesto de un gasto bastante más pequeño ( en kWh ) de lo que podéis leer en el ejemplo de factura que se muestra en la imagen de arriba.

ENUNCIADO 1.1
(1) El precio de la energía eléctrica en enero de 2021 llegó a ser de $0,136$ euros por cada kilovatio-hora ( kWh ) consumido. Además del gasto propiamente dicho, una cierto distribuidor de energía eléctrica - llamémosle A - cobró a cada cliente $20$ euros en conceptos varios (tasa de potencia y otros conceptos varios). Con estos datos, escríbase la función, $y=f(x$), que describe el coste ( para el consumidor ) en función de la cantidad de energía consumida, $x$ ( en kWh ). Si un cliente consumió una cantidad de energía de $800$ kWh, ¿ cuánto tuvo que pagar ?.

SOLUCIÓN
Como hay una relación de proporcionalidad directa entre la cantidad de energía y coste de la misma ( más el servicio debido a distribución, mantenimiento, y otros conceptos ) la función pedida es lineal de tipo lineal afín (1) $$f(x)=0,136x+20$$ La cantidad total a pagar, según los datos del enunciado, es $f(800)=0,136·800+20=128,80\,\text{euros}$

Observación 1: Ésta es una función lineal afín, y su gráfica es una recta que no pasa por el origen de coordenadas. Si deseásemos comparar la oferta que nos hiciese otra compañía distribuidora, podríamos decidir a cambiar a la nueva distribuidora si, a partir de un gasto regular estimado, y al representar ambas rectas en el mismo diagrama cartesiano, los puntos de la segunda recta quedasen por debajo de los de la primera ( con el mismo valor de la abscisa ) para valores de ésta mayores que las del punto de intersección de las dos rectas.

Observación 2: El precio del kWh varía, básicamente debido a los vaivenes de la oferta y la demanda. Por ejemplo, en días de viento la producción eléctrica por parte de los parques de aerogeneradores, los precios bajan. En el ejemplo de cálculo hemos supuesto un precio alto, pues, desgraciadamente, así están las cosas.


-oOo-
Continuación ...
ENUNCIADO 1.2
(2) Otro distribuidor de energía eléctrica, B, vende cada kilovatio-hora ( kWh ) a $0,114$, y cobra 25 euros en conceptos varios ( tasa de potencia, etcétera ). A partir de qué cantidad de energía consumida le convendría a un cliente aceptar la oferta de B ( y rechazar la de A ) ?.

SOLUCIÓN
La función lineal afín que nos da el coste para el cliente es ahora $$g(x)=0,114x+25$$ Representando las funciones $f$ y $g$ en un mismo diagrama cartesiano - que hemos realizado con la ayuda de GeoGebra - permite entender mejor el significado d ela pregunta del enunciado ( ved la figura que sigue ).

Observamos que para consumos superiores a los $227,27\,\text{kWh}$, es más económica la oferta de B ( para el consumidor que la de A ); ahora bien, si el consumo es inferior a esa cantidad, es preferible seguir con el distribuidor A como proveedor.

Observación 3:
No es necesario representar la gráfica para calcular el consumo ( en kWh ) por encima del cual conviene aceptar la oferta de B: basta resolver el sistema de ecuaciones dado por $$\left\{\begin{matrix}y&=&0,136x&+&20\\ \\y&=& 0,114x&+&25\end{matrix}\right.$$ donde hemos denotado por $y$ los valores de salida ( costes ) de sendas funciones, obteniendo - fácilmente - la solución ( las coordenadas del punto de intersección de las dos rectas ): $$\left\{\begin{matrix}x=227,27\,\text{kWh} \\ \\ y=50,91\,\text{euros}\end{matrix}\right.$$

Observación 4:
Según los datos del ENUNCIADO 1, al cliente le conviene contratar al distribuidor ( o proveedor ) B, pues el gasto de energía, $800\,\text{kWh}$, es mayor que la abscisa del punto de corte, $227,27\,\text{kWh}$. De esta forma, el coste sería de $g(800)=0,114·800+25=116,2\,\text{euros} \prec f(300)=128,80\,\text{euros}$ $\square$

Celdas de combustible. Del hidrógeno a la electricidad

El hidrógeno y los motores eléctricos Hay dos maneras de utilizar el hidrógeno para obtener la energía que mueva el motor (de un vehículo, por ejemplo). Una de ellas, la más explosiva - nunca mejor dicho -, consiste en utilizar el hidrógeno (por ejemplo a partir del propergol) como combustible en un motor de combustión, además del oxígeno, claro, como comburente. Dichos motores son propios de cohetes para situar una nave espacial en órbita, no de otro tipo de vehículos. Son muchos los problemas de este tipo de motor, el principal es su peligrosidad por la posibilidad de explosionar el hidrógeno, su alto consumo de combustible y su alto nivel de ruido, principalmente su peligrosidad, puesto que además, una vez iniciada la reacción no se puede detener hasta haber agotado el combustible. Los motores eléctricos de pila de hidrógeno. La otra forma de utilizarlo, sin explosiones, sin gases contaminantes ni altas temperaturas, se basa en la obtención de una corriente eléctrica a partir de una reacción de oxidación-reducción que como, únicos reactivos requiere hidrógeno y oxígeno. Dicha reacció proporciona energía eléctrica que luego, de forma ya muy conocida, se convierte en energía mecánica mediante un motor eléctrico. Muy probablemente los motores de combustión y los motores de explosión estén llamados a ir dejando paso a esta nueva generación de sistemas de propulsión. Así mismo, la pila de hidrógeno puede utilizarse para almacenar energía (química), facilmente convertible en eléctrico cuando la necesitemos; es por ello que en un futuro, posiblemente incluso llegue a sustituir las baterías convencionales, algunas de ellas muy contaminantes (por su contenido en metales pesados: niquel, cadmio, mercurio, plomo). Dichos dispositivos reciben nombres equivalentes: "pila de hidrógeno", "celdas de combustible", o "pilas de combustible", entre otras. Una celda de combustible consiste básicamente en una membrana catalizadora (actualmente suele ser polimérica) conductora de protones (iones de hidrógeno cargados positivamente) que separa el ánodo del cátodo y hace las veces de electrolito. Para que esto funcione se necesita, como reactivos, hidrógeno y oxígeno (el contenido en el aire del ambiente). Los electrodos, ánodo y cátodo, a diferencia de los de una batería que reaccionan y se alteran, en una pila de combustible son catalíticos - propician la reacción pero no intervienen en ella, luego, son, en principio, estables químicamente. En el lado del ánodo, el hidrógeno esparcido en el catalizador se disocia en protones y electrones. Los primeros van a parar al cátodo, a través de la membrana de polímero conductor que hace las veces de electrólito, y los electrones circulan por el circuïto externo (he aquí la corriente eléctrica que movera el motor (eléctrico, claro). Por otra parte, en el cátodo, los protones reaccionan con las moléculas de oxígeno del aire, dando como producto de la reacción vapor de agua y, claro, calor. El rendimiento de una pila de combustible que funcione con hidrógeno (70 ) suele ser más bajo que el de una batería convencional (90 ), pero las ventajas son evidentes (contaminación - por lo menos en cuanto a la reacción en sí se refiere - nula y motores más limpios y silenciosos). Cada pila (celda) de combustible crea una tensión de 0,8 V, aproximadamente. Por lo tanto se suelen agrupar en serie para obtener la tensión necesaria para mover un motor eléctrico. Hay muchas esperanzas depositadas en esta tecnología, en especial, atendiendo los efectos paliativos del cambio climático originado por las sociedades humanas tecnificadas. Cómo almacenar el hidrógeno en un vehículo ? Por supuesto, el almacenamiento del hidrógeno es uno de los procesos clave. El hidrógeno se encuentra en estado gaseoso en condiciones normales de presión y temperatura. Hasta ahora, se ha almacenado el hidrógeno licuado, con lo que, para ello se requiere muy alta presión. A bordo del vehículo, ello entraña peligro, coste y dificultades. Uno de los objetivos es precisamente coseguir almacenar el hidrógeno de forma que puedan evitarse estos importantes problemas. Ya de por sí, tal cosa sería inviable en determinados tipos de vehículos (un automovil o una pequeña embarcación, por ejemplo). Pero, hay otra forma de hacerlo: la adsorción de hidrógeno entre las moléculas de nuevos materiales (nanoporosos). Muchos equipos de investigación en Ciencias de Materiales están persiguiendo este objetivo. Se está investigando con materiales compuestos de carbón activado, zeolitas y arcillas apilaradas. Estos materiales cumplen cuatro requisitos: tienen resistencia mecánica y son seguros, además de ser ligeros y barato. Se utilizaron ya las pilas de combustible en el proyecto Apolo (NASA) que llevó al ser humano a pisar la Luna hace ya casi 40 años (en concreto la pila AFC, acrónimo de "alkaline fuell cell", sin embargo, su auge se ha visto enlentecido por directrices económicas y políticas que gobiernan el mundo. Existen ya submarinos que están provistos de pilas de combustible y que les conceden una gran autonomia y habitabilidad. Visto como va todo en lo que se refiere a la necesidad de reducir las emisiones de dióxido de carbono a la atmosfera, parece probable que las celdas de combustible sustituirán también a las baterías convencionales en un futuro no muy lejano de forma generalizada, con lo cual se reducirá la contaminación por metales pesados (plomo, cadmio, mercurio ...), materiales que en las baterías y pilas convencionales se usan como electrodos y que, claro, se alteran químicamente. El hidrógeno puede obtenerse de la disociación de la molécula de agua, invirtiendo energía de otras fuentes; de ahí, por ejemplo, los paneles de células fotovoltaicas que haría las veces de "gasolinera" para las celdas de combustible al ayudar a suministrar la energía necesaria para romper las moléculas de agua e ir llenando así el depósito de hidrógeno. También se puede obtener el hidrógeno de otras moléculas que lo contengan - diesel, metanol, etcétera -, pero claro, en ese caso, hay otros productos de reacción, como por ejemplo, el dióxido de carbono. En cualquier caso, todo esto, amigos, tiene mucho futuro, especialmente, si pensamos en aplicarlo a los motores auxiliares de nuestros veleros. Queda, por supuesto, mucho camino por recorrer.

¿ Qué ocurre cuando quemamos algo ?

Ejemplo 1.
La siguiente situación puede ayudarnos a reflexionar. El carbono se quema gracias al oxígeno, produciendo dióxido de carbono, mediante la reacción química $$C\, \text{( sólido )} + O_{2}\, \text{(gas)} \rightarrow CO_{2}\,\text{(gas)} + \text{energía en forma de calor}$$ ¿ Qué masa ( en gramos ) de oxígeno ( $O_{2}$ ) hace falta para quemar $6\,\text{kg}$ de carbón ? ¿ Qué cantidad ( masa, en gramos ) de dióxido de carbono se produce en tal caso ?

SOLUCIÓN.
Consulando la tabla periódica, vemos que la masa molar del carbón es de $12\,\dfrac{\text{g}}{\text{mol}}$; la del oxígeno ($O_2$ ), de $2\cdot 16 \,\dfrac{\text{g}}{\text{mol}}=32 \,\dfrac{\text{g}}{\text{mol}}$; y la del dióxido de carbono, $12\,\dfrac{\text{g}}{\text{mol}}+2\cdot 16\,\dfrac{\text{g}}{\text{mol}} = 44\,\dfrac{\text{g}}{\text{mol}}$

Entonces, cantidad de carbono ( en moles ) es igual a $$ 6 \,\text{kg de } C \cdot 1000 \,\dfrac{g}{\text{kg}}\cdot \dfrac{1}{12}\,\,\dfrac{\text{moles de carbono}}{\text{g}}=500\,\text{moles de C}$$
Y, según los coeficientes estequiométricos de la reacción ( que son igual a $1$, todos ellos ), la cantidad de moles de $O_2$ es
$$500\,\text{moles de } C \cdot \dfrac{1}{1}\,\dfrac{\text{moles de } O_2}{\text{moles de } C} = 500 \,\text{moles de }C$$ Por tanto, según los coeficientes estequiométricos de la ecuación química, la cantidad de $CO_2$ que se produce ( en moles ) es:
$500\,\text{moles de carbono}\cdot \dfrac{1}{1}\,\dfrac{\text{moles de }CO_2}{\text{mol de } O_2}=500\,\text{moles de } CO_2$

Y, finalmente, la cantidad ( en gramos ) de $CO_2$ ( dióxido de carbono ) producida es:
$500\,\text{moles de } CO_2 \cdot \dfrac{44}{1}\,\dfrac{\text{g de } CO_2}{\text{moles de } CO_2} = 22\,000\, \text{g de } CO_2 = 22\,\text{kg de } CO_2$
$\square$

Ejemplo 2.
Un combustible fosil muy empleado es el gas propano ( $C_{3}\,H_{8}$ ). Al quemarse con oxígeno ( $O_2$ ) da lugar a dióxido de carbono ( $CO_{2}$ ), agua ( $H_{2}O$ ), y ( naturalmente ) energía en forma de calor. ¿ Qué masa ( en gramos ) de oxígeno ( $O_{2}$ ) hace falta para quemar $6\,\text{kg}$ de propano ? ¿ Qué cantidad ( masa, en gramos ) de dióxido de carbono se produce en este otro caso ? ¿ Qué cantidad de agua ( $H_{2}O $ ) ?

SOLUCIÓN. La reacción ( con los coeficientes estequiométricos ) es $$C_{3}H_{8}\, \text{( gas )} + 5\,O_{2}\, \text{(gas)} \rightarrow 3\,CO_{2}\,\text{(gas)} + 4\,H_{2}O \,\text{(gas)} + \text{energía en forma de calor}$$ Recordemos las masas molares de los componentes de la reacción:
$CO_2: 12\,\dfrac{\text{g de C}}{\text{mol de }C}+2\cdot 16\,\dfrac{\text{g de }O}{\text{mol}} = 44 \,\dfrac{\text{g de } CO{2}}{\text{mol de }CO_2}$
$C_{3}H_{8}: 3\cdot 12\,\dfrac{\text{g de C}}{\text{mol de }C}+8 \cdot 1\,\dfrac{\text{g de }O}{\text{mol}} = 44 \,\dfrac{\text{g de } C_{3}H_{8}}{\text{mol de }C_{3}H_{8}}$
$O_2: 2\cdot 16\,\dfrac{\text{g de O}}{\text{mol de }O} = 32 \,\dfrac{\text{g de } O_2}{\text{mol de }O_2}$
$H_{2}O: 2\cdot 1\,\dfrac{\text{g de H}}{\text{mol de }H}+1 \cdot 16\,\dfrac{\text{g de }O}{\text{mol de} O} = 18 \,\dfrac{\text{g de } H_{2}O}{\text{mol de }H_{2}O}$
Entonces,
$ 6 \,\text{kg de } C_{3}H_8 \cdot 1000 \,\dfrac{\text{g de} C_{3}H_8}{\text{kg de } C_{3}H_8} \cdot \dfrac{1}{44}\,\,\dfrac{\text{moles de }C_{3}H_8}{\text{g de} C_{3}H_8}=\dfrac{1500}{11}\,\text{moles de }C_{3}H_8 \approx$
$\approx 136\,\text{moles de }C_{3}H_8\,\text{consumidos}$
luego, según los coeficientes estequiométricos de la reacción, las cantidades involucradas son: $$ \dfrac{1500}{11}\,\text{moles de }C_{3}H_8 \cdot \dfrac{5}{1}\,\dfrac{\text{moles de }O_2}{\text{moles de }C_{3}H_8 }\cdot \dfrac{32}{1}\,\dfrac{\text{g de }O_2}{\text{mol de}O_2}\approx 8\,727\,\text{g de }O_2\, \text{consumidos}$$ $$ \dfrac{1500}{11}\,\text{moles de }C_{3}H_8 \cdot \dfrac{3}{1}\,\dfrac{\text{moles de }CO_2}{\text{moles de }C_{3}H_8 }\cdot \dfrac{44}{1}\,\dfrac{\text{g de }CO_2}{\text{mol de}CO_2}\approx 18\,000\,\text{g de }CO_2\, \text{producidos}$$ $$ \dfrac{1500}{11}\,\text{moles de }C_{3}H_8 \cdot \dfrac{4}{1}\,\dfrac{\text{moles de }H_{2}O}{\text{moles de }C_{3}H_8 }\cdot \dfrac{18}{1}\,\dfrac{\text{g de}H_{2}O}{\text{mol de}O_2}\approx 9\,818\,\text{g de }H_{2}O\, \text{producidos}$$
$\square$

Conceptos básicos de electroquímica. La pila Daniell

Una pila o cel·la electroquímica, transforma energia química en energia elèctrica (i viceversa) mitjançant una reacció d'oxidació-reducció. En el cas d'una pila, el resultat és un corrent continu d'electrons que flueix ( pel circuit exterior ) des de l'ànode (1) de la pila (born negatiu), on es produeix l'oxidació del material de l'elèctrode, al càtode de la pila (born positiu), elèctrode on es produeix la reducció (guany d'electrons). En aquest article es mostra l'exemple de la pila Daniell per raons didàctiques; no obstant això, les idees que s'exposen són comunes a qualsevol cel·la electroquímica, incloses les piles d'hidrògen.

És ben sabut que els portadors de càrrega elèctrica a través d'un conductor són els electrons [1]. Més endavant, justificarem el sentit del moviment dels electrons pel conductor exterior que connecta els dos borns d'una pila, i que van de l'ànode, $A$, al càtode, $C$. Com que el sistema es conservatiu es compleix que la quantitat de treball deguda a les forces internes per desplaçar l'electró és igual a la quantitat oposada al canvi d'energia potencial en anar de l'ànode al càtode, es a dir: $$W_{\text{forces internes del sistema}}=-\Delta\,E\overset{\text{def}}{=}-(E_{\text{C}}-E_{\text{A}})=E_{A}-E_{C}$$
Sabem que un electró que circuli pel conductor que conecta el born negatiu (ànode de la pila) amb el born positiu (càtode de la pila) augmenta la seva energia cinètica a mesura que s'acosta al born positiu, per tant, pel teorema de les forces vives, $W_{\text{forces internes del sistema}}=\Delta\,K \succ 0$ ( on $\Delta \, K$ és la variació de l'energía cinètica de l'electró), que, naturalment, es positiva; llavors, $E_{A}-E_{C} \succ 0$ i per tant $E_{A} \succ E_{C}$ ( com es ben evident, ben pensat, sense necessitat d'escriure cap expressió matemática ), es a dir, l'energia potencial de l'electró quan surt de l'ànode ( born negatiu de la pila ) és més gran que la que té quan arriba a al càtode ( born positiu de la pila ). El mateix podem dir si ens posem en dos punts qualssevol del recorregut: si el portador es mou de $P_i$ a $P_f$, és degut a que l'energia potencial de l'electró en el punt $P_i$ és més gran que la que té en el punt $P_f$: $E_{P_i} \succ E_{P_f}$.

D'altra banda, cal que hi hagi una diferència de potencial elèctric lligada amb la variació d'energia potencial del portador de càrrega entre dos punts del camp elèctric, de tal manera que la variació d'energia potencial és igual a la variació de potencial elèctric, $\Delta V$, multiplicada pel valor de la càrrega elèctrica del portador, $Q$: $$E_{P_i}-E_{P_f}=Q\cdot (V_{P_i}-V_{P_f}) \succ 0 \quad \quad (1)$$

Si la càrrega del portador es positiva, és clar que $V_{P_i} \succ V_{P_f}$, car $E_{P_i} \succ E_{P_f}$, la qual cosa facilita en bona part la resolució dels circuits elèctrics/electrònics aplicant la llei d'Ohm. Aquesta és una de les raons per la qual encara es fa servir l'anomenat sentit convencional del corrent: pel conductor que conecta els dos borns de la pila, fem la consideración que els portadors tenen càrrega positiva i circulen desde el born positiu al born negatiu. Llavors és clar que $V_{C}\succ V_{A}$, és a dir, el potencial en el born positiu de la pila, $C$, es més gran que el potencial en el born negatiu, $A$. A mida que anem entrant en matèria (electroquímica) parlarem d'això en profunditat.

Ara bé, com que els portadors reals ( electrons ) tenen càrrega negativa, cal tenir en compte que, de (1), en ésser la diferencia d'energía potencial entre l'ànode i el càtode, $E_{A}-E_{C} \succ 0$ tenim que $E_{A}-E_{C}=Q\cdot (V_{A}-V_{C}) \succ 0$, però como que ara $Q \prec 0$, es dedueix que $(V_{A}-V_{C})$ també ha de ser una quantitat negativa, i, per tant, $V_{A} \prec V_{C}$; i, en general, entre dos punts qualssevol: $V_{P_i}\prec V_{P_f}$.

La diferencia en valor absolut de potencial elèctric entre els dos elèctrodes (borns de la pila), $|V_A - V_C|$, s'anomena força electromotriu de la pila (que abreujarem FEM), i que, juntament amb el temps durant el qual la pila pot estar donant una determinada intensitat de corrent elèctric, en dóna les característiques funcionals.

La FEM d'una pila (la diferència de potencial entre els dos elèctrodes de la pila (ànode i càtode) es mesura en volts. Efectivament, només cal comprovar que, dimensionalment, [FEM] = [energia]/[càrrega elèctrica] = [potencial elèctric], que, en unitats del sistema internacional, vindrà donat en volts (V). Pel que fa a la capacitat de la pila o bateria, se sol donar en ampères x hora (Ah), indicant així la quantitat de temps, mesurat en hores, durant el qual la pila pot subministrar una determinada intensitat de corrent abans que la reacció d'oxidació-reducció ja no pugui mantenir-se, moment en el qual, la pila o bateria es considera esgotada. Així, per exemple, de la indicació d'una bateria caracteritzada per una capacitat de 80 Ah, podem entendre, a tall indicatiu, que és capaç de donar un corrent elèctric de, per exemple, 0,8 A durant 100 h sense interrupció.

És evident que això equival a pensar en la pila o bateria com un "dipòsit" de càrrega elèctrica en continu moviment pel circuït exterior i que es consumeix en alimentar els aparells elèctrics que hi estan connectats. Sabent el valor de la potència d'aquests aparells podem fer una estimació del temps durant el qual la pila o bateria proporcionarà corrent abans que es decarregui. Considerem, per exemple, una bateria de 12 V i 80 Ah (completament carregada) a la qual hi connectem una làmpada de 8 watts (W) de potència. Com que 1 W = 1 V x 1 A, tan sols cal que resolem una senzilla proporció: el temps estimat que tardarà a descarregar-se aquesta bateria serà de 120 hores, tal i com podem comprovar fent 80 A h x 12 V / (8 W) = 120 h

Amb el terme càtode - terme que prové del grec i que significa "camí de descéns" - (introduït per William Whewell el 1834, a partir de la lectura dels treballs de Faraday), es fa referència a l'elèctrode on es produeix la semireacció de reducció ( guany d'electrons per part del material d'aquest, els cuals provenen del circuit exterior ). A l'interior de la pila, el ions carregats positivament (cations) - provinents de l'oxidació del material de l'ànode - es dirigeixen envers el càtode, captant aquest electrons del circuit exterior. L'etimologia del terme ànode - que també prové del grec i fou emprat per primera vegada per Faraday -, ve a significar “camí d'ascéns”. Així, avui en dia és ben sabut que mentre que el corrent de portadors de càrrega a l'interior de la pila, és a dir, a través de l'electròlit, és iònic, per fora (pel tram de conductor extern que tanca el circuït) és electrònic; però això no se sabia en els temps de Faraday. Com que els cations (ions amb càrrega positiva) es dirigeixen a través de l'electròlit envers el càtode ( born negatiu de la pila ), els primers investigadors varen pensar que pel fil conductor el corrent anava en el mateix sentit, car cal tenir en compte que quan es van descobrir les primeres piles encara no es tenia coneixment de l'existència dels electrons com a portadors de càrrega en els materials conductors del fil metàl·lic que conectava els dos borns de la pila. És per això que es prengué i, sovint, ara per raons pràctiques, encara es continua prenent el conveni que considera el moviment del corrent en un circuit elèctri o electrònic com si de portadors de càrrega positiva es tractés (pel circuït exterior de la pila): de l'ànode (born positiu de la pila ) al càtode (born negatiu de la pila), sabent però que els veritables portadors de càrrega que actuen en el fil conductor d'un circuït (alimentat per la pila) son els electrons i, per tant, són aquests els que circulen realment del càtode a l'ànode (sentit real de circulació del corrent en un circuït) pel fil conductor que conecta els dos borns de la pila.

Els elèctrodes són barres metàl·liques (o bé d'algun òxid, o de grafit) i cada un està submergit en una dissolució iònica, ja sigui líquida o bé, tal com es fabriquen les modernes piles i bateries, en forma gel; per això, es parla sovint d'interfícies, fent referència a la superfície de contacte metall-electròlit. El metall de l'ànode té un valor de potencial estàndard menor que el del càtode per tal que es produeixi la reacció d'oxidació-reducció. Cada interfície es pot considerar una subpila, havent-hi un solució iònica en cada una on s'hi troben submergits els elèctrodes respectius.

Per exemple, una pila Daniell (vegeu la figura de sota) en la seva versió moderna consta de dos receptacles ( subcel·les ), on els elèctrodes estan submergits en una dissolució en aigua: de sulfat de coure força concentrada en la part del càtode (CuSO₄), i de sulfat de zinc (ZnSO₄) poc concentrada en la part de l'ànode. Ambdues parts de la pila es comuniquen per un envà porós o pont salí: un tub en forma porós en forma de U que permet l'intercanvi iònic entre les dues cubetes, evitant així que entrin en contacte directe les dues dissolucions, ja que la reacció directa entre els dos electròlits faria minvar el rendiment de la pila. Els ponts salins es poden fer preparant una dissolució saturada de nitrat potasi (KNO₃) a una temperatura elevada, de tal manera que en deixar-se refredar, aquesta queda gelifica i saturada d'ions. La funció del pont salí és important: permet mantenir l'equilibri dinàmic de càrrega elèctrica entre ambdos parts de la pila.

font de la imatge: Wikipedia, https://es.wikipedia.org/wiki/Pila_Daniell

Evidentment, la pila deixarà de donar corrent quan la concentració d'ions Zn⁺⁺ en l'electròlit assoleixi un valor que impedeixi que el zinc continuï dissolent-se. Una pila Daniell proporciona una FEM aproximada d'1 volt.

La tendència que té un material a reduir-se es mesura mitjançant el potencial de reducció (també anomenat potencial estàndard), de tal manera que entendrem que com més alt sigui el valor d'aquest, més capacitat de reducció tindrà i, per tant, més oxidació produirà en l'ànode. Prenent com a zero de potencial un elèctrode estàndard d'hidrogen (EEH): 0 V (a 25º C i concentracions de les substàncies en dissolució igual a la unitat) es realitzen els experiments per determinar els potencials de reducció d'altres substàncies en la interfície o cel·la galvànica amb l'elèctrode d'hidrogen i, així, es poden elaborar les taules de potencial estàndard (potencial de reducció) per a cada substància. Aquests valors poden ser positius o negatius; per exemple, el coure (Cu) té un potencial EEH de 0,337 V, mentre el zenc (Zn) té un potencial de -0,763 V. Mirant aquestes taules hom pot saber quin serà el material que es redueix i quin el que s'oxida en una cel·la galvànica (pila): el que té un potencial més alt serà el que té major tendència a reduir-se (l'oxidant) i, doncs, farà de càtode; i l'altre (el que té menor potencial de reducció) serà el reductor (s'oxidarà) i, per tant, farà d'ànode. La diferència entre el potencial del càtode i el de l'ànode dóna el valor de la FEM; així, en el cas de la pila Daniell, trobem que aquest és igual aproximadament a 1 V (FEM = 0,337-(-0,763) = 1,100 V) [2].

La circulació global de portadors de càrrega (circulació iònica-electrònica) és el resultat de la conversió de l'energia química en energia elèctrica gràcies a una reacció d'oxidació-reducció, i constitueix genèricament el que entenem per una pila electroquímica, sovint, formada en realitat per un conjunt de cel·les electroquímiques disposades en sèrie-paral·lel per obtenir un valor òptim de capacitat de càrrega i la FEM adequada. En aquest sentit, és important apuntar que la capacitat de càrrega de la pila depèn de la grandària de la pila, i el valor de la FEM, de la reacció concreta d'oxidació-reducció que hi té lloc.


-oOo-
Observacions:
(1) La polaritat del càtode depèn del tipus de dispositu: si es tracta d'un receptor, aquest té polaritat negativa (como es el cas d'un diode en un circuit electric/electrònic, o bé d'una cubeta electrolítica); i, en el cas d'una pila el càtode té polaritat positiva car correspon a l'elèctrode de la subcel·la on té lloc la semireacció de reducció. L'ànode, per tant, té polaritat positiva si el dispositiu és un receptor ( en un circuit ), i es conecta al born negatiu de la pila, és a dir, a l'ànode de la pila, que s'oxida en el procés de descàrrega d'aquesta. És per consegüent un error pensar que el càtode té sempre polaritat negativa i que l'ànode té sempre polaritat positiva.
(2) La conversió d'energia elèctrica en energia química constitueix el procés invers: el càtode en el procés de recàrrega de la pila és ara l'elèctrode que en el procés de descàrrega era l'ànode, i viceversa. Parlem aleshores d'acumuladors. Aquest procés invers és necessari per poder recarregar el dispositiu i permetre que torni a funcionar como a pila.
(3) També es pot fer servir l'electròlisi ( reacció d'oxidació-reducció ) per recubrir un material ( que actúa como a càtode, como ara el ferro ) amb una fina capa d'un altre metall que actúa com a ànode ( com ara, el coure ), submergits ambdós en una dissolució ácida y conectats als borns d'una pila: el càtode de la cubeta electrolítca al born negatiu de la batería i l'ànode al born positiu d'aquesta. El gruix de la capa que es diposita sobre el material on es produeix la reducción depèn del temps que ha circulat el corrent pel bany electrolític i de la intensitat del corrent que suministra la pila. I, també es pot fer servir aquest procés d'electròlisi (invers al de les piles) per treure l'òxid de la superficie de les peces metàl·liques rovellades. Per altra banda, l'electròlisi és tambié la causa de la corrosió galvànica.

---------
[1] Això és pot justificar a partir del model de bandes de conducció i comprovar experimentalment interpretant l'efecte Hall.

[2] Gairebé en tots els manuals de Química podeu consultar les taules dels potencials estàndard de reducció; jo he consultat el llibre de Bruce H. Mahan (pàgina 265): Química. Curso Universitario Fondo Educativo Interuniversitario, 1977

Baterías de plomo-ácido: https://es.wikipedia.org/wiki/Bateías_de_plomo_y_ácido, Wikipedia


Baterías de plomo-ácido: https://es.wikipedia.org/wiki/Bateías_de_plomo_y_ácido, Wikipedia

Polea con masa no despreciable; esto es: gira al deslizar por su ranura un cuerda con tensión

En ambos casos, las cuerdas están enrolladas en las correspondientes partes cilíndricas de la polea; éstas, por tanto, giran solidariamente por efecto del peso de los cuerpos que cuelgan de los extremos. En el primer caso, ambas cuerdas se desenrollan en el mismo sentido; en el segundo, mientras una se enrolla ( la que corresponde al cuerpo de menor masa que cuelga de ella ), la otra ( de la que pende el cuerpo de mayor masa ) se desenrolla. En cualquiera de los dos casos, la polea ( formada por los dos cilindros unidos en una sola pieza ) gira siempre en el mismo sentido. En cada una de las situaciones ( reseñadas en la imagen con A y B ), y a partir de los datos ( los radios de los dos cilindros que componen la polea, las masa de los cuerpos que cuelgan de las cuerdas, el momento de inercia de la polea ) los respectivos sistemas de ecuaciones planteados permiten calcular las tensiones, las aceleraciones lineales y la aceleración angular de la polea.

Polea sin masa (idealización), esto es: sin que gire al deslizarse por ella una cuerda

En la parte superior de la fotografía de la pizarra se trata el estudio del caso de una polea ideal de masa nula ( que no gira ) y en la inferior el caso de una polea con masa no despreciable ( considerando su giro ). En el primer caso (la polea no gira y la cuerda se desliza sin rozamiento por la ranura), con los datos del problema ( el radio de la polea y las masa de los cuerpos que cuelgan de la cuerda), el sistema de ecuaciones planteado permite calcular la tensión de la cuerda y la aceleración lineal de los cuerpos, que naturalmente es la misma. En el segundo caso ( la polea gira ), partiendo de los datos ( momento de inercia de la polea, masa de los dos cuerpos que cuelgan de la cuerda ), el sistema de ecuaciones planteado permite calcular las tensiones, la aceleración lineal y la aceleración angular de la polea.

Utilizando el error relativo

Enunciado:
¿Qué error porcentual se comete al sustituir el seno de $20^{\circ}$ por el valor de dicho ángulo expresado en radianes ? Repetir el mismo cálculo para el caso de la tangente.

Solución:

Sea el valor nominal de una cierta magnitud, $x^{*}$, y denominemos por $x$ un valor aproximado de $x^{*}$. Entonces, se define el error absoluto de la aproximación $x \approx x^{*}$ como
    $E=\left|x-x^{*}\right|$
y el error relativo de la forma
    $e=\dfrac{E}{x^{*}}\approx \dfrac{E}{x}$

  (a)
Expresemos el valor del ángulo dado en radianes:
    $20^{\circ}=20\cdot \dfrac{\pi}{180}=\dfrac{\pi}{9}\,\text{rad}$
entonces, al hacer la aproximación
    $\sin\,\dfrac{\pi}{9} \approx \dfrac{\pi}{9}$
obtenemos el siguiente error absoluto
    $E=\left|\sin\,\dfrac{\pi}{9}-\dfrac{\pi}{9}\right|\approx 0,007046$
siendo el error relativo
    $e=\dfrac{\dfrac{\pi}{9}}{\sin\,\dfrac{\pi}{9}} \approx 0,0206 \rightarrow 2,06 \,\% $

  (b)
De la aproximación
    $\tan\,\dfrac{\pi}{9} \approx \dfrac{\pi}{9}$
obtenemos el siguiente error absoluto
    $E=\left|\tan\,\dfrac{\pi}{9}-\dfrac{\pi}{9}\right|\approx 0,014904$
siendo el error relativo
    $e=\dfrac{\dfrac{\pi}{9}}{\tan\,\dfrac{\pi}{9}} \approx 0,040949 \rightarrow 4,09 \,\% $

Referencias: Ejercicio ( 1.6, página 14 ) propuesto en el libro de J.L. Meriam, Mecánica para Ingenieros, Editorial Reverté, Barcelona, 1988.

$\square$

Un trozo de cadena deslizándose por el borde de una mesa ...

ENUNCIADO
Sobre una mesa reposa un trozo de cuerda ( de densidad lineal, $\delta$, homogénea ), de longitud $l$. Una parte de dicha cuerda cuelga por el borde de la mesa, formando la cuerda un ángulo recto con la arista/borde. El coeficiente de rozamiento de la mesa con la cuerda es $\mu$. Calcúlese la velocidad, $v$, de un punto de la cuerda cuando, en su caída, el extremo que reposaba sobre la mesa pasa por el borde.

SOLUCIÓN
Supondremos que la cuerda empieza a caer con velocidad inicial nula ( equilibrio ) y, por tanto, esto se produce para una cierta longitud del tramo que cuelga, que denominaremos $x_0$. Teniendo en cuenta el principio de conservación de la energía mecánica, y despreciando la pérdida por disipación de calor debida al roce de la cuerda con la mesa, el cambio de energía cinética, $\Delta\,K$, debe ser igual al trabajo realizado, $\Delta\,W$, por la fuerza activa que actúa sobre la cuerda y que da lugar al movimiento de la misma - desde que empieza el movimiento hasta la situación pedida en el enunciado - ( Teorema de las fuerzas vivas ), esto es, $$\Delta\,K=\Delta\,W$$ por tanto $$\dfrac{1}{2}\,m\,v^2-\dfrac{1}{2}\,m\cdot 0^2=\displaystyle \int_{x_0}^{l}\,F(x)\,dx$$ y como la masa, $m$, de la cuerda es $m=\delta\,l$, podemos escribir $$ \dfrac{1}{2}\,\delta\,l\,v^2=\displaystyle \int_{x_0}^{l}\,F(x)\,dx \quad \quad \quad \quad \quad \quad \quad \quad (1)$$
siendo $x$ la longitud de cuerda que cuelga por el borde en cada instante de tiempo

Calculemos el valor de $x_0$ imponiendo la condición de equilibrio: $$g\,(l-x_0)\,\delta\,\mu = x_0\,\delta\,g$$
y de aquí encontramos $$x_0=\dfrac{\mu}{\mu+1}\,l$$

Por otra parte, la función que describe la fuerza global que actúa sobre la cuerda para cada valor de $x$ es $$F(x)=\delta\,g\,x- \delta\,g\,\mu\,(l-x)$$ esto es $$F(x)=\delta\,g\,\left((\mu+1)\,x-\mu\,l\right)$$ Así, el segundo miembro de (1) es igual a $$\displaystyle \delta\,g\,\,\int_{\frac{\mu}{\mu+1}\,l}^{l}\,\left((\mu+1)\,x-\mu\,l\right)\,dx $$ y por, el Primer y el Segundo Teoremas Fundamentales del Cálculo, obtenemos como resultado de dicha integral definida $$\dfrac{1}{2}\,\dfrac{\delta\,g\,l^2}{\mu+1}$$ por lo que la igualdad (1) nos queda $$\dfrac{1}{2}\,\delta\,l\,v^2=\dfrac{1}{2}\,\dfrac{\delta\,g\,l^2}{\mu+1}$$ así que, despejando $v$, llegamos a $$v=\sqrt{\dfrac{g\,l}{\mu+1} }$$

Así, por ejemplo, si $\mu =0,8$ y $l=0,5\, \text{m}$, la longitud del trozo de cuerda que cuelga cuando empieza el movimiento ( posición de equilibrio ) es de $x_0=\dfrac{0,8}{0,8+1}\cdot 0,5 \approx 0,22 \, \text{m}$, y la velocidad de un punto de la cuerda cuando el extremo izquierdo de la misma abandona la mesa es igual a $\sqrt{\dfrac{9,81 \cdot 0,5}{0,8+1}} \approx 1,65\, \dfrac{\text{m}}{\text{s}}$

$\square$

Utilizando el teorema de las fuerzas vivas

ENUNCIADO
El vector de posición en cada instante de tiempo de un cuerpo ( que consideramos puntual ) en movimiento en el espacio, cuaya masa es igual a la unidad, viene dado por $$\vec{r}(t)=t^4\,\vec{i}-t^3\,\vec{j}+t^2\,\vec{k}$$ ( las unidades corresponden a las del Sistema Internacional ). ¿ Cuál es el trabajo realizado por la fuerza que actúa sobre dicho cuerpo entre $t_1=2 \, \text{s}$ y $t_2=3 \, \text{s}$ ?.

SOLUCIÓN
Por el Teorema de las fuerzas vivas, el incremento de energía cinética entre dos instantes de tiempo debe ser igual al trabajo realizado por las fuerzas del sistema actuando sobre dicho cuerpo entre estos dos instantes, esto es $$\Delta\,K = \Delta\,W \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1)$$ donde el segundo miembro de la igualdad es $$\Delta\,K = \dfrac{1}{2}\,m\,v_{2}^2-\dfrac{1}{2}\,m\,v_{1}^2 \quad \quad \quad \quad \quad \quad \quad \quad (2) $$ siendo $v_{1} \equiv \left\|\vec{v}(2)\right\|$ y $v_{2} \equiv \left\|\vec{v}(2)\right\|$, con lo cual, $v_{1}^2 = \left(\left\|\vec{v}(2)\right\|\right)^2$ y $v_{2}^2 = \left(\left\|\vec{v}(3)\right\|\right)^2$

Para hallar estas dos cantidades, debemos calcular, primero, la función vectorial velocidad instantánea, así que debemos derivar la función vectorial de posición instantánea: $$\vec{v}(t) \equiv \dfrac{d\vec{r}(t)}{dt}=4\,t^3\,\vec{i}-3\,t^2\,\vec{j}+2\,t\,\vec{k}$$ y, particularizando en los dos instantes dados, obtenemos $$\vec{v}(3) =4\cdot 3^3\,\vec{i}-3\cdot 3^2\,\vec{j}+2\cdot 3\,\vec{k}=108\,\vec{i}-27\,\vec{j}+6\,\vec{k}$$ y $$\vec{v}(2) =4\cdot 2^3\,\vec{i}-3\cdot 2^2\,\vec{j}+2\cdot 2\,\vec{k}=32\,\vec{i}-12\,\vec{j}+4\,\vec{k}$$ Calculándo, ahora, el cuadrado de los módulos de sendos vectores: $$v_{2}^2 \equiv \left(\left\|\vec{v}(3)\right\|\right)^2=108^2+(-27)^2+6^2=12429$$ y $$v_{1}^2 \equiv \left(\left\|\vec{v}(2)\right\|\right)^2=32^2+(-12)^2+4^2=1184$$ Así, pues, de (1), y teniendo en cuenta (2), el valor del trabajo pedido es $$\Delta\,W=\dfrac{1}{2}\cdot 1 \,(12429-1184)=5625,5\,\text{J}$$
$\square$

Ones transversals

En actuar sobre un medi elàstic i continu mitjançant una pertorbació externa hom cedeix a aquest una certa energia la qual es propagarà a través de les partícules materials que el constitueixen. Considerem, doncs, un medi continu i elàstic a través del qual es transmet una pertorbació periòdica que anomenarem ona harmònica, la forma matemàtica de la qual determinarem.

En actuar sobre un medi elàstic i continu mitjançant una pertorbació externa hom cedeix a aquest una certa energia la qual es propagarà a través de les partícules materials que el constitueixen. Considerem, doncs, un medi continu i elàstic a través del qual es transmet una pertorbació periòdica que anomenarem ona harmònica, la forma matemàtica de la qual determinarem.

[ cliqueu aquí per interactuar amb la construcció ]

És convenient, per començar, distingir entre dos tipus de pertorbacions: els polsos, i les ones pròpiament dites. Els polsos, quant a la forma d'aportar energia al medi (de causar la pertorbació), són impulsos limitats en el temps, mentre que les ones es poden entendre com el resultat de reiterar l'impuls de forma continuada en el temps. Pensem, per exemple, en una corda de longitud indefinida estirada al terra; en agafar un extrem de la corda i fer-la moure en la direcció vertical, donant-li un impuls (de forma sobtada), s'obté un pols que es propaga al llarg de la corda; si mantenim el moviment oscil·latori de la mà amb què transmetem l'energia a la corda es produeix el que entendrem per ona harmònica.

Situant l'origen de coordenades d'un sistema d'eixos cartesians en un punt convenient, estudiarem l'estat de vibració de les partícules P del medi lineal unidimensional (que s'estén al llarg de l'eix Ox) en la direcció transversal a la de propagació (la de l'eix Oy) de la pertorbació a través d'aquest (moviment harmònic simple [que abreviarem MHS]).

Si entenem que la direcció de propagació és la de l'eix Ox, el moviment oscil·latori dels punts P es produeix, per tant, en la direcció Oy. Dit això, podem escriure que l'elongació de la partícula P, situada a la distància x de l'origen (focus) de la pertorbació de la forma

y(t₁,x_P)=A sin( w t₁)

on A representa l'elongació màxima o amplitud; w, la freqüència angular del MHS que descriu la partícula; i t₁, el temps propi del MHS de P (amb què mesurem les elongacions que en la direcció vertical va prenent la partícula P).

El sistema de referència el situem en la posició del focus i al seu temps propi l'anomenarem t. Recordem que el nostre objectiu consisteix a estudiar el moviment de P (situat a una distància x de O) en funció del temps t del sistema de referència i en la direcció Oy; és a dir, pretenem trobar una expressió y(t,x), amb la qual cosa, de fet, si ho apliquem no solament a un punt, sino a tots els punts {P} haurem donat l'equació del moviment MHS de tots i cada un dels punts del medi continu unidimensional (situats damunt de l'eix Ox): l'equació de l'ona harmònica.

Cal tenir en compte que la pertorbació tarda un temps t₂ en arribar a la posició de P des del focus (al llarg de l'eix Ox), per tant podem escriure el temps t₁ de la forma t - t₂
és a dir
y(t,x) = A sin( w (t - t₂)       [1]

Com que la pertorbació viatja en la direcció de l'eix Ox (direcció de propagació) a una certa velocitat v (velocitat de propagació) és evident que

t₂ = x/v, on x representa la coordenada de posició del punt considerat, per tant podem escriure [1] de la forma:

y(t,x) = A sin(w(t-x/v))

o de forma equivalent

y(t,x) = A sin(wt - (w/v)x).

Interpretem la quantitat w/v com el nombre d'ones completes compreses en un segment de l'eix Ox d'una determinada longitud i designem aquesta quantitat (nombre d'ona) amb la lletra k.

És per això que, sovint, escriurem l'equació d'ones de la forma

y(t,x) = A sin( wt - kx) on el terme kx es pot entendre com el desfasament (diferència de fase) de la vibració en el punt situat a distància x respecte del punt situat l'origen (x=0).

Tot el que hem dit es pot estendre a medis de més d'una dimensió. Pensem, per exemple, les ones que es produeixen en la superfície d'un estany (ones en un medi bidimensional), o les ones de so en propagar-se per l'espai tridimensional. $\diamond$

Psicrómetro

Psicrómetro ( aparato para medir la humedad relativa )Altafulla, Tarragonaverano de 2004

Algunos efectos de la luz en la cena